Stress-Strain Tensor Constitutive Equation Calculator (Isotropic Material)

Stress–Strain Tensor Constitutive Equation (Isotropic Material)

In continuum mechanics, the stress–strain tensor constitutive equation defines how a material responds to applied loads by relating the stress components to the corresponding strains within a body. For isotropic materials, which have identical mechanical properties in all directions, this relationship is both linear and symmetric, simplifying the complex behavior of solids under deformation. The equation embodies Hooke’s Law in three dimensions, using tensor notation to account for normal and shear components of stress and strain.

The isotropic constitutive model involves two independent material constants—Young’s modulus (E) and Poisson’s ratio (ν). These parameters describe the stiffness and the lateral deformation behavior of the material. By using these constants, the calculator computes the full stress or strain tensor under general three-dimensional loading conditions, ensuring accurate predictions of material response. This formulation is fundamental in finite element analysis (FEA), structural design, and material modeling, where it serves as the cornerstone for determining how elastic materials deform and recover under multi-axial states of stress.

Constitutive Equation for Isotropic Material (Hook’s Law)

Compute Strain Tensor

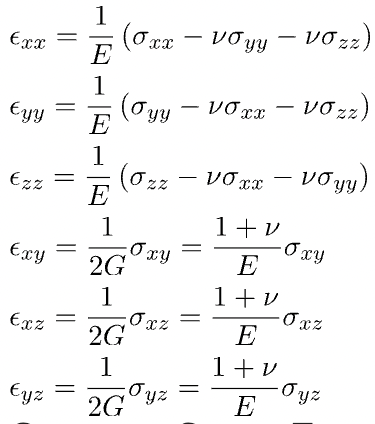
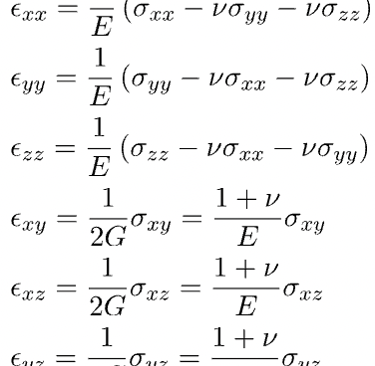
Compute Stress Tensor